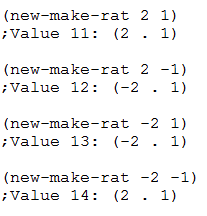第二章 构造数据抽象 2.1 数据抽象引导 EX 2.1 1 2 3 4 5 (define (new-make-rat n d) (let ((g (gcd n d))) (cond ((or (and (< n 0) (< d 0)) (and (> n 0) (< d 0))) (cons (- (/ n g)) (- (/ d g)))) (else (cons (/ n g) (/ d g))))))
EX 2.2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 (define (make-segment start end) ;构造函数make-segment (cons start end)) (define (start-segment segment) ;选择函数start-segment (car segment)) (define (end-segment segment) ;选择函数end-segment (cdr segment)) (define (make-point x y) ;构造函数make-point (cons x y)) (define (x-point point) ;选择函数x-point (car point)) (define (y-point point) ;选择函数y-point (cdr point)) ;求线段中点 (define (midpoint-segment segment) (let ((start (start-segment segment)) (end (end-segment segment))) (make-point (/ (+ (x-point start) (x-point end)) 2) (/ (+ (y-point start) (y-point end)) 2))))
1 2 3 4 5 ;测试程序 (define start (make-point 1 3)) (define end (make-point 4 3)) (define seg (make-segment start end)) (define mid (midpoint-segment seg))
EX 2.3 两种矩形表示,一种采用两对线段(4条),另一种采用两条相邻线段(2条),主要设计抽象屏障,这里只采用后一种。当然还有别的表示方法,如三点表示 (我没有仔细研究)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 (define (make-rect seg1 seg2) ;构造函数,构造矩形 (cons seg1 seg2)) (define (seg1-in-rect rect) ;选择函数,相邻的一条边a (car rect)) (define (seg2-in-rect rect) ;选择函数,相邻的另一条边b (cdr rect)) (define (a-length rect) ;a的长度 (let ((a (seg1-in-rect rect))) (let ((a-startpt (start-segment a)) (a-endpt (end-segment a))) (let ((a-x1 (x-point a-startpt)) (a-y1 (y-point a-startpt)) (a-x2 (x-point a-endpt)) (a-y2 (y-point a-endpt))) (sqrt (+ (square (abs (- a-x1 a-x2))) (square (abs (- a-y1 a-y2))))))))) (define (b-length rect) ;b的长度 (let ((b (seg2-in-rect rect))) (let ((b-startpt (start-segment b)) (b-endpt (end-segment b))) (let ((b-x1 (x-point b-startpt)) (b-y1 (y-point b-startpt)) (b-x2 (x-point b-endpt)) (b-y2 (y-point b-endpt))) (sqrt (+ (square (abs (- b-x1 b-x2))) (square (abs (- b-y1 b-y2))))))))) (define (area-rect rect) ;计算面积,参数是矩形 (let ((a (a-length rect)) (b (b-length rect))) (* a b))) (define (perimeter-rect rect) ;计算周长,参数是矩形 (let ((a (a-length rect)) (b (b-length rect))) (* (+ a b) 2)))
1 2 3 4 5 6 7 8 9 10 ;测试程序 ;(define p1 (make-point 1 2)) ;p1 p2 p3,边不平行于坐标轴的矩形 ;(define p2 (make-point 2 3)) ;(define p3 (make-point 3 1)) (define p1 (make-point 1 1)) ;p1 p2 p3,边平行于坐标轴的矩形 (define p2 (make-point 1 3)) (define p3 (make-point 5 1)) (define rectangle ;测试所用的矩形 (make-rect (make-segment p1 p2) (make-segment p1 p3)))
EX 2.4 根据代换法则,分析一下这种过程性表示方式
1 2 3 4 (define (cons x y) (lambda (m) (m x y))) (define (car z) (z (lambda (p q) p)))
(car (cons x y)) ——>
(car (lambda (m) (m x y))) ——>
((lambda (m) (m x y)) (lambda (p q) p)) ——>
((lambda (p q) p) x y) ——>
x代入具体的数字
(car (cons 1 2)) ——>
((lambda (p q) p) 1 2) ——>
1 由代换结果分析,不难写出cdr的过程性表示
1 2 (define (cdr z) (z (lambda (p q) q)))
EX 2.5 (cons 2 3) = 108 = 2 * 2 * 3 * 3 * 3
1 2 3 4 5 6 7 8 9 10 11 12 (define (cons x y) (* (expt 2 x) (expt 3 y))) (define (car z) (if (= 0 (remainder z 2)) (+ (car (/ z 2)) 1) 0)) (define (cdr z) (if (= 0 (remainder z 3)) (+ (cdr (/ z 3)) 1) 0))
EX 2.6 根据书中给出的zero和add-1
1 2 3 4 (define zero (lambda (f) (lambda (x) x))) (define (add-1 n) (lambda (f) (lambda (x) (f ((n f) x)))))
推导出one(one = zero + add-1)
(add-1 zero) ——>
(add-1 (lambda (f) (lambda (x) x))) ——>
(lambda (f)
(lambda (x)
(f (
((lambda (f) (lambda (x) x)) f) x)))) ——>
(lambda (f)
(lambda (x)
(f
((lambda (x) x) x)))) ——>
(lambda (f)
(lambda (x)
(f x))) ——>
得到one的定义1 2 3 4 (define one (lambda (f) (lambda (x) (f x))))
同理,求two的定义。two = one + add-1
(add-1 one) ——>
(add-1 (lambda (f) (lambda (x) (f x)))) ——>
(lambda (f)
(lambda (x)
(f ((n f) x)))) ——>将n代换为one
(lambda (f)
(lambda (x)
(f ((
(lambda (f) (lambda (x) (f x))) f)
x)))) ——>化简lambda (f)
(lambda (f)
(lambda (x)
(f ( (lambda (x) (f x)) x)))) ——>化简lambda (x)
(lambda (f)
(lambda (x)
(f (f x)))) ——>
得到two的定义1 2 3 4 (define two (lambda (f) (lambda (x) (f (f x)))))
根据zero,one,two的定义
1 2 3 4 5 6 7 8 9 10 11 12 (define zero ;no f (lambda (f) (lambda (x) x))) (define one ;one f (lambda (f) (lambda (x) (f x)))) (define two ;two f (lambda (f) (lambda (x) (f (f x)))))
据此推导加法过程定义(对此仍不太懂,没有理解FP,柯里化之类的内容)
1 2 3 4 5 (define church-add (lambda (m n) (lambda (f) (lambda (x) (m f (n f x))))))