第二章 构造数据抽象
2.2 层次性数据和闭包性质
EX 2.24
1
| (define 2-24 (list 1 (list 2 (list 3 4))))
|
解释器打印出:
(1 (2 (3 4)))
盒子指针结构:
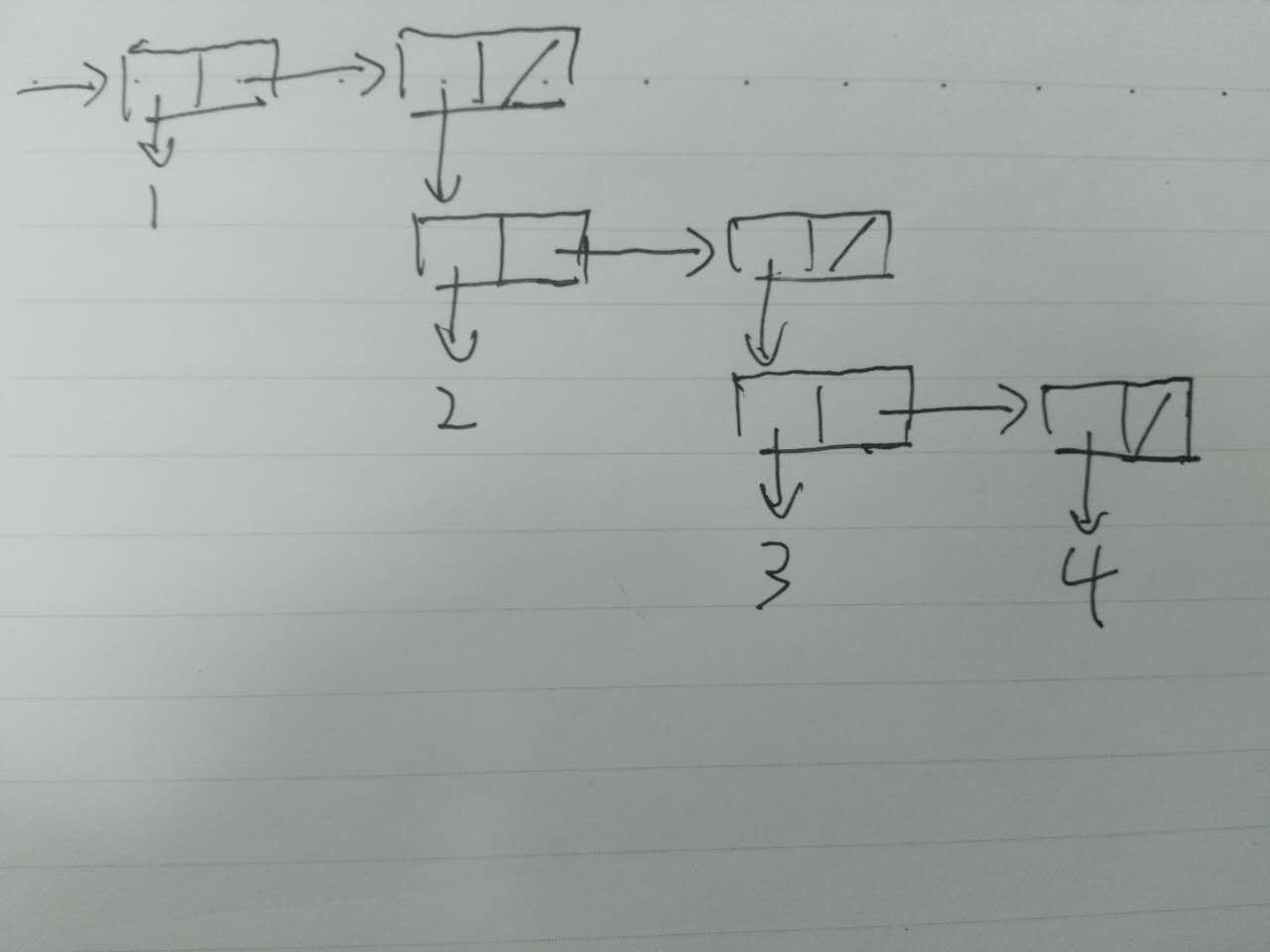
EX 2.25
1
2
3
4
5
6
7
8
9
10
11
| (define a1 (list 1 3 (cons 5 7) 9))
(define 2-25-1
(cdr (car (cdr (cdr a1))))) ;(cdr (car (cdr (cdr a1)))) 等价于 (cdaddr a1)
(define a2 (list (list 7)))
(define 2-25-2
(car (car a2))) ;(car (car a2)) 等价于 (caar a2)
(define a3 (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7)))))))
(define 2-25-3
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr a3))))))))))))) ;等价于 (cadadr (cadadr (cadadr a3)))
|
EX 2.26
1
2
| (define x (list 1 2 3))
(define y (list 4 5 6))
|
打印结果如下:
(append x y) -> (1 2 3 4 5 6)
(cons x y) -> ((1 2 3) 4 5 6)
(list x y) -> ((1 2 3) (4 5 6))
EX 2.27
1
2
3
4
5
6
7
| ;原始reverse
(define (reverse x)
(define (iter rest result)
(if (null? rest)
result
(iter (cdr rest) (cons (car rest) result))))
(iter x '()))
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| ;处理二叉树、三叉树等,如(list (list 2 1) (list 4 3) (list 6 5))
(define (deep-reverse x)
(define (iter rest result)
(if (null? rest)
result
(iter (cdr rest)
(cons (if (pair? (car rest))
(deep-reverse (car rest))
(car rest))
result))))
(iter x '()))
;一种更好的算法
(define (better-deep-reverse x)
(if (pair? x)
(reverse (map better-deep-reverse x))
x))
|
EX 2.28
1
2
3
4
5
| (define (fringe x)
(cond ((null? x) '())
((not (pair? x)) (list x))
(else (append (fringe (car x)) ;left branch
(fringe (cdr x)))))) ;right branch
|
EX 2.29
1
2
3
4
5
| ;原始构造函数
(define (make-mobile left right)
(list left right))
(define (make-branch length structure)
(list length structure))
|
1
2
3
4
| ;测试程序
(define lfbran (make-branch 1 2))
(define rtbran (make-branch 2 (make-mobile (make-branch 3 4) (make-branch 5 6))))
(define test-mobile (make-mobile lfbran rtbran))
|
a) 根据原始构造函数,不难写出选择函数
1
2
3
4
5
6
7
8
| (define (left-branch mobile)
(car mobile))
(define (right-branch mobile)
(cadr mobile))
(define (branch-length branch)
(car branch))
(define (branch-structure branch)
(cadr branch))
|
b) total-weight 计算活动体总重量,递归地求和左右分支的总重量
1
2
3
4
5
6
7
8
| (define (total-weight mobile)
(+ (branch-weight (left-branch mobile))
(branch-weight (right-branch mobile))))
(define (branch-weight branch) ;计算分支重量
(if (pair? (branch-structure branch)) ;是否吊着活动体
(total-weight (branch-structure branch))
(branch-structure branch)))
|
c) check-balance 检查二叉活动体是否平衡,递归判断左右分支是否平衡
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| (define (cal-torque branch) ;计算分支力矩
(* (branch-length branch) (branch-weight branch)))
(define (check-balance mobile)
(if (null? mobile)
#t
(let ((left (left-branch mobile))
(right (right-branch mobile)))
(and (torque-equal? left right)
(branch-balance? left)
(branch-balance? right)))))
(define (torque-equal? lfbranch rtbranch) ;力矩是否相等
(= (cal-torque lfbranch) (cal-torque rtbranch)))
(define (branch-balance? branch) ;分支是否平衡
(if (pair? (branch-structure branch)) ;是否吊着活动体
(check-balance (branch-structure branch))
#t))
|
d) 这就是数据抽象的好处,改变构造方式,我们只需要修改相应的选择函数
1
2
3
4
5
6
7
8
| (define (new-left-branch mobile)
(car mobile))
(define (new-right-branch mobile)
(cdr mobile))
(define (new-branch-length branch)
(car branch))
(define (new-branch-structure branch)
(cdr branch))
|
EX 2.30
1
2
3
4
5
6
| ;直接定义
(define (square-tree1 tree)
(cond ((null? tree) '())
((not (pair? tree)) (square tree))
(else (cons (square-tree1 (car tree))
(square-tree1 (cdr tree))))))
|
1
2
3
4
5
6
7
| ;map和递归定义
(define (square-tree2 tree)
(map (lambda (sub-tree)
(if (pair? sub-tree)
(square-tree2 sub-tree)
(square sub-tree)))
tree))
|
EX 2.31
1
2
3
4
5
6
7
| (define (tree-map proc items)
(cond ((null? items) '())
((not (pair? items)) (proc items))
(else (cons (tree-map proc (car items))
(tree-map proc (cdr items))))))
(define (square-tree3 tree)
(tree-map square tree))
|
EX 2.32
求集合S的子集,就是求(cdr S)和(cdr S)里的每个元素append (car S)
例如S:(list 1 2 3),子集是(() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))
先求(2 3)的子集,(() (3) (2) (2 3)),然后给每个append 1
具体递归分析如下:
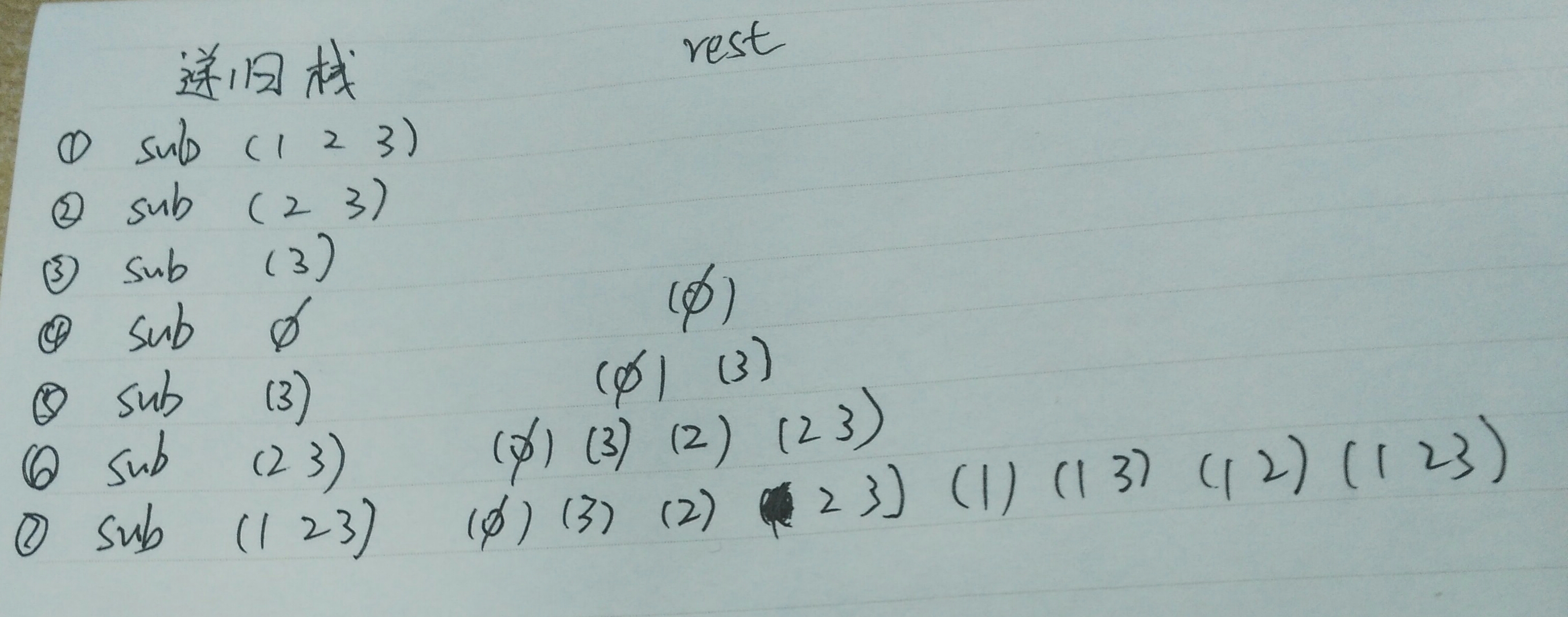
1
2
3
4
5
6
| (define (subsets s)
(if (null? s)
(list '())
(let ((rest (subsets (cdr s))))
(append rest (map (lambda (x) (cons (car s) x))
rest)))))
|