Java 的中文编码问题(1)

发表于 2017-02-09 | 分类于 Java

引自《深入分析Java中的中文编码问题》

问题引入

计算机中存储信息的最小单元是一个字节即 8 个 bit，所以能表示的字符范围是 0~255 个
人类要表示的符号太多，无法用一个字节来完全表示
要解决这个矛盾必须需要一个新的数据结构 char，从 char 到 byte 必须编码

常见的编码格式

ASCII
ASCII 码，总共有 128 个，用一个字节的低 7 位表示，0~~31 是控制字符如换行回车删除等；32~~126 是打印字符，可以通过键盘输入并且能够显示出来。
ISO-8859-1
128 个字符显然是不够用的，于是 ISO 组织在 ASCII 码基础上又制定了一些列标准用来扩展 ASCII 编码，它们是 ISO-8859-1~ISO-8859-15，其中 ISO-8859-1 涵盖了大多数西欧语言字符，所有应用的最广泛。ISO-8859-1 仍然是单字节编码，它总共能表示 256 个字符。
GB2312
它的全称是《信息交换用汉字编码字符集基本集》，它是双字节编码，总的编码范围是 A1-F7，其中从 A1-A9 是符号区，总共包含 682 个符号，从 B0-F7 是汉字区，包含 6763 个汉字。
GBK
全称叫《汉字内码扩展规范》，是国家技术监督局为 windows95 所制定的新的汉字内码规范，它的出现是为了扩展 GB2312，加入更多的汉字，它的编码范围是 8140~FEFE（去掉 XX7F）总共有 23940 个码位，它能表示 21003 个汉字，它的编码是和 GB2312 兼容的，也就是说用 GB2312 编码的汉字可以用 GBK 来解码，并且不会有乱码。
GB18030
全称是《信息交换用汉字编码字符集》，是我国的强制标准，它可能是单字节、双字节或者四字节编码，它的编码与 GB2312 编码兼容，这个虽然是国家标准，但是实际应用系统中使用的并不广泛。
UTF-16
UTF-16 具体定义了 Unicode 字符在计算机中存取方法。UTF-16 用两个字节来表示 Unicode 转化格式，这个是定长的表示方法，不论什么字符都可以用两个字节表示，两个字节是 16 个 bit，所以叫 UTF-16。UTF-16 表示字符非常方便，每两个字节表示一个字符，这个在字符串操作时就大大简化了操作，这也是 Java 以 UTF-16 作为内存的字符存储格式的一个很重要的原因。
UTF-8
UTF-16 统一采用两个字节表示一个字符，虽然在表示上非常简单方便，但是也有其缺点，有很大一部分字符用一个字节就可以表示的现在要两个字节表示，存储空间放大了一倍，在现在的网络带宽还非常有限的今天，这样会增大网络传输的流量，而且也没必要。而 UTF-8 采用了一种变长技术，每个编码区域有不同的字码长度。不同类型的字符可以是由 1~6 个字节组成。
UTF-8 有以下编码规则：
- 如果一个字节，最高位（第 8 位）为 0，表示这是一个 ASCII 字符（00 - 7F）。可见，所有 ASCII 编码已经是 UTF-8 了。
  - 如果一个字节，以 11 开头，连续的 1 的个数暗示这个字符的字节数，例如：110xxxxx 代表它是双字节 UTF-8 字符的首字节。
  - 如果一个字节，以 10 开始，表示它不是首字节，需要向前查找才能得到当前字符的首字节

Java中的编解码

解码：字节->字符　　编码：字符->字节

IO中的编解码

根据处理数据类型的不同分为：字符流(byte) 字节流(char)
根据数据流向不同分为：输入流(读，外存->内存) 输出流(写，内存->外存)
字符流：Reader，Writer
字节流：InputStream, OutputStream
桥梁：InputStreamReader(字节->字符) OutputStreamWriter(字符->字节)

InputStreamReader具体的解码由 StreamDecoder 实现，将字节解码成字符，解码过程中必须由用户指定 Charset 格式。值得注意的是如果你没有指定 Charset，将使用本地环境中的默认字符集，例如在中文环境中将使用 GBK 编码。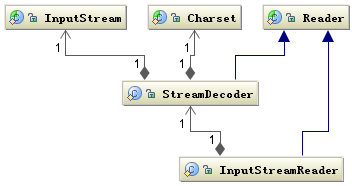
"Input"

同样，OutputStreamWriter具体的编码由 StreamEncoder 实现，将字符编码成字节，编码格式和默认编码规则与解码是一致的。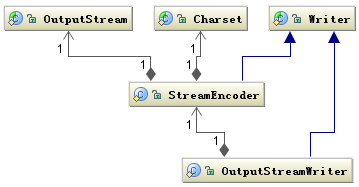
"Output"

String file = "c:/stream.txt"; 
String charset = "UTF-8";  // 编码格式

// 写字符换转成字节流
FileOutputStream outputStream = new FileOutputStream(file);
OutputStreamWriter writer = new OutputStreamWriter( 
outputStream, charset);
try { 
   writer.write("这是要保存的中文字符"); 
} finally { 
   writer.close(); 
} 

// 读取字节转换成字符
FileInputStream inputStream = new FileInputStream(file); 
InputStreamReader reader = new InputStreamReader( 
inputStream, charset); 
StringBuffer buffer = new StringBuffer(); 
char[] buf = new char[64]; 
int count = 0; 
try { 
   while ((count = reader.read(buf)) != -1) { 
       buffer.append(buffer, 0, count); 
   } 
} finally { 
   reader.close(); 
}

内存中的编解码

在 Java 开发中除了 I/O 涉及到编码外，最常用的应该就是在内存中进行字符到字节的数据类型的转换，Java 中用 String 表示字符串，所以 String 类就提供转换到字节的方法，也支持将字节转换为字符串的构造函数。如下代码示例：

1
2
3

String s = "这是一段中文字符串"; 
byte[] b = s.getBytes("UTF-8"); 
String n = new String(b,"UTF-8");

另外一个是已经被被废弃的 ByteToCharConverter 和 CharToByteConverter 类，它们被 Charset 类取代。Charset 提供 encode 与 decode 分别对应 char[] 到 byte[] 的编码和 byte[] 到 char[] 的解码。如下代码所示：

1
2
3

Charset charset = Charset.forName("UTF-8"); 
ByteBuffer byteBuffer = charset.encode(string); 
CharBuffer charBuffer = charset.decode(byteBuffer);

Java中具体的编解码实例

public class IOTest {
    public static void main(String... args) {
        String s = "I am 君山";
        encode(s);
    }

    public static void encode(String s) {
        toHex(s.toCharArray());
        try {
            byte[] iso8859 = s.getBytes("ISO-8859-1");
            toHex(iso8859, "iso8859");
            byte[] gb2312 = s.getBytes("GB2312");
            toHex(gb2312, "gb2312");
            byte[] gbk = s.getBytes("GBK");
            toHex(gbk, "gbk");
            byte[] utf16 = s.getBytes("UTF-16");
            toHex(utf16, "utf16");
            byte[] utf8 = s.getBytes("UTF-8");
            toHex(utf8, "utf8");
        } catch (UnsupportedEncodingException e) {
            e.printStackTrace();
        }
    }

    private static void toHex(char[] c) {
        System.out.println("-------- char[] --------");
        String s = "";
        for (int i = 0; i < c.length; i++)
            s += Integer.toHexString(c[i]) + " ";
        System.out.println(s);
    }

    private static void toHex(byte[] b, String charset) {
        System.out.println("------" + charset + "-------");
        for (int i = 0; i < b.length; i++) {
            System.out.printf("%x", b[i]);
            System.out.print(" ");
        }
        System.out.println();
    }
}

打印结果如下

-------- char[] --------
49 20 61 6d 20 541b 5c71 
------iso8859-------
49 20 61 6d 20 3f 3f 
------gb2312-------
49 20 61 6d 20 be fd c9 bd 
------gbk-------
49 20 61 6d 20 be fd c9 bd 
------utf16-------
fe ff 0 49 0 20 0 61 0 6d 0 20 54 1b 5c 71 
------utf8-------
49 20 61 6d 20 e5 90 9b e5 b1 b1

ISO-8859-1

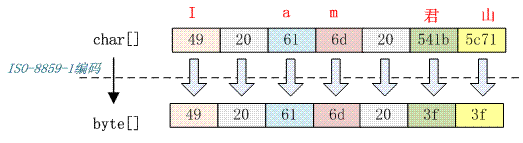
7 个 char 字符经过 ISO-8859-1 编码转变成 7 个 byte 数组，ISO-8859-1 是单字节编码，中文“君山”被转化成值是 3f 的 byte。3f 也就是“？”字符，所以经常会出现中文变成“？”很可能就是错误的使用了 ISO-8859-1 导致的。中文字符经过 ISO-8859-1 编码会丢失信息，通常我们称之为“黑洞”，它会把不认识的字符吸收掉。由于现在大部分基础的 Java 框架或系统默认的字符集编码都是 ISO-8859-1，所以很容易出现乱码问题。
GB2312

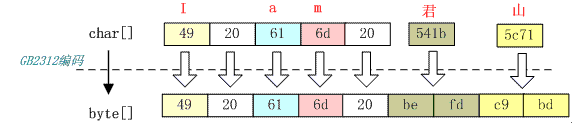
GB2312 字符集有一个 char 到 byte 的码表，不同的字符编码就是查这个码表找到与每个字符的对应的字节，然后拼装成 byte 数组。如果查到的码位值大于 oxff 则是双字节，否则是单字节。双字节高 8 位作为第一个字节，低 8 位作为第二个字节
GBK

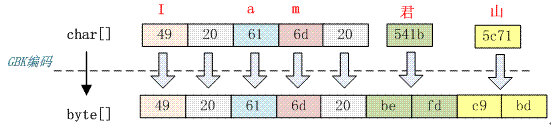
与 GB2312 编码的结果是一样的，由此可以得出 GBK 编码是兼容 GB2312 编码的，它们的编码算法也是一样的。不同的是它们的码表长度不一样，GBK 包含的汉字字符更多。所以只要是经过 GB2312 编码的汉字都可以用 GBK 进行解码，反过来则不然。
UTF-16

用 UTF-16 编码将 char 数组放大了一倍，单字节范围内的字符，在高位补 0 变成两个字节，中文字符也变成两个字节。从 UTF-16 编码规则来看，仅仅将字符的高位和地位进行拆分变成两个字节。特点是编码效率非常高，规则很简单，由于不同处理器对 2 字节处理方式不同，Big-endian（高位字节在前，低位字节在后）或 Little-endian（低位字节在前，高位字节在后）编码，所以在对一串字符串进行编码是需要指明到底是 Big-endian 还是 Little-endian，所以前面有两个字节用来保存 BYTE_ORDER_MARK 值。(UTF16打印结果中的前两个字节fe ff，因为在Windows平台下默认的Unicode编码为Little-endian的UTF-16)UTF-16 是用定长 16 位（2 字节）来表示的 UCS-2 或 Unicode 转换格式，通过代理对来访问 BMP 之外的字符编码。
UTF-8

UTF-16 虽然编码效率很高，但是对单字节范围内字符也放大了一倍，这无形也浪费了存储空间，另外 UTF-16 采用顺序编码，不能对单个字符的编码值进行校验，如果中间的一个字符码值损坏，后面的所有码值都将受影响。而 UTF-8 这些问题都不存在，UTF-8 对单字节范围内字符仍然用一个字节表示，对汉字采用三个字节表示。

UTF-8 编码与 GBK 和 GB2312 不同，不用查码表，所以在编码效率上 UTF-8 的效率会更好，所以在存储中文字符时 UTF-8 编码比较理想。

几种编码格式的比较

对中文字符后面四种编码格式都能处理，GB2312 与 GBK 编码规则类似，但是 GBK 范围更大，它能处理所有汉字字符，所以 GB2312 与 GBK 比较应该选择 GBK。UTF-16 与 UTF-8 都是处理 Unicode 编码，它们的编码规则不太相同，相对来说 UTF-16 编码效率最高，字符到字节相互转换更简单，进行字符串操作也更好。它适合在本地磁盘和内存之间使用，可以进行字符和字节之间快速切换，如 Java 的内存编码就是采用 UTF-16 编码。但是它不适合在网络之间传输，因为网络传输容易损坏字节流，一旦字节流损坏将很难恢复，想比较而言 UTF-8 更适合网络传输，对 ASCII 字符采用单字节存储，另外单个字符损坏也不会影响后面其它字符，在编码效率上介于 GBK 和 UTF-16 之间，所以 UTF-8 在编码效率上和编码安全性上做了平衡，是理想的中文编码方式。

Hexo的NexT主题默认显示侧边栏

发表于 2016-05-05 | 分类于 Hexo

用Hexo的Next主题有一段时间了，但是发觉边框栏即便设置了 sidebar: always，也不能自动展开

在网上查了查，找到了解决办法

在 \themes\next\source\js\motion_global.js 做如下修改：

sidebarToggle: function (integrator) {
    sidebarToggleMotion.init();
    integrator.next();
    // 可以不加if直接显示
    // 加if的话，要在主题配置文件里面修改 sidebar: always
    if (CONFIG.sidebar === 'always') {
       // 模拟点击一下侧边栏按钮
       sidebarToggleMotion.clickHandler();
    }
}

哈哈，边框栏可以自动展开啦！开心

PHP+MySql+Apache+WordPress Win10 配置

发表于 2016-05-04 | 分类于搭建环境

闲话少说，首先是安装，但是版本的选择很重要。

PHP 5.6

当然是官网啦！

“php1”

这里选择5.6的版本，PHP 7太新了，怕兼容性出现问题。点击Windows downloads

版本有Thread Safe/Non Thread Safe 和 X86 X64的两种组合，随自己的喜欢了。Non Thread Safe不会检查线程是否安全。这里下载的是Zip格式的压缩包

“php2”

解压缩，我的路径是 F:\php5.6 复制份php.ini-development，并改名为PHP.ini，用记事本打开

查找 extension_dir 将

;extension=php_mysql.dll
;extension=php_mysqli.dll

前面的注释符”;”去掉，使PHP支持mysql

Apache 2.4

点这里下载！这里选择2.4版本，因为和PHP 5.6一样都是在vc11下编译的

“apache1”

点击 Files for Microsoft Windows，这里有五个版本，第一项ApacheHaus是个第三方下载平台，在它的网站下载独立的Apache压缩包。另外四个中，第二个也是独立的Apache下载地址，另外三个是集成开发环境。这里直接选择了第一个

“apache2”

解压缩，我的路径是 F:\Apache24 接下来的工作就是比较主要的了，配置 httpd.conf

修改监听端口

如果原有80端口被其他服务占用，可以修改 Listen 80 为 Listen 8081 (例如)

修改权限

apache 2.4 不再支持deny/allow 等指令，改用 denied/granted，将denied改为granted，或者注释掉重写。
否则会出现的一个问题是 You don’t have permission to access / on this server
如果根目录下没有index文件，也会出现这个问题

<Directory />
    AllowOverride none
    # Require all denied
	Require all granted
</Directory>

DocumentRoot "${SRVROOT}/htdocs" 改为自己的目录
例如我的 DocumentRoot "D:/PHPWeb"

支持PHP

在配置文件最后添加以下代码，配置php的module 和 php.ini 的路径

# php5 support
LoadModule php5_module "F:/php5.6/php5apache2_4.dll"
AddHandler application/x-httpd-php .php
# configure the path to php.ini
PHPIniDir "F:/php5.6"

启动Apache

在bin目录下执行httpd.exe，正常情况就是没有信息返回

“apache3”

在 D:/PHPWeb 内新建 index.php, 内容填入以下PHP代码

<?php Echo "Hello, CJW!";?>

此时可以在浏览器输入localhost:8081/index.php，可以看到打印的结果，此时PHP+Apache已经搭建好

“apache4”

WordPress

点这里下载，我选择zip版本，然后解压缩

官网教程写的也比较清楚，主要有几个步骤需要注意

上传WordPress到一个远程主机

教程里说的这一步，可以把zip解压到根目录里，例如我的 "D:\PHPWeb\wordpress"

设置 wp-config.php

将 wp-config-sample.php 改名为 wp-config.php，然后就是配置数据库，教程里写的很清楚。

测试

在浏览器里输入 http://localhost:8081/wordpress/ 进行测试，第一次访问是注册界面

如果出现 You don’t have permission to access / on this server 检查Apache配置，或者看是否缺少index文件

“wp”

MySql 5.6

安装过程基本一路next，注意填入的用户名和密码要记住，在wp-config.php配置时需要填入

SICP 2.2节习题(4)

发表于 2016-05-03 | 分类于 SICP解题集

第二章构造数据抽象

2.2 层次性数据和闭包性质

书中P82页，嵌套映射部分

;二元组
(define (flatmap proc seq)
  (accumulate append '() (map proc seq)))
(define (prime-sum? pair)
  (prime? (+ (car pair) (cadr pair))))
(define (make-pair-sum pair)
  (list (car pair) (cadr pair) (+ (car pair) (cadr pair))))

(define (prime-sum-pairs n)
  (map make-pair-sum
       (filter prime-sum?
               (flatmap
                (lambda (i)
                  (map (lambda (j) (list i j))
                       (enumerate-interval 1 (- i 1))))
                (enumerate-interval 1 n)))))

P33页判断是否为素数

;P33 prime?
(define (prime? n)
	(define (smallest-divisor n)
		(find-divisor n 2))
	(define (find-divisor n test-divisor)
		(cond ((> (square test-divisor) n) n)
			  ((divides? test-divisor n) test-divisor)
			  (else (find-divisor n (+ test-divisor 1)))))
	(define (divides? a b)
		(= (remainder b a) 0))
	(= n (smallest-divisor n)))

(define (permutations s)
  (if (null? s)
      (list '())
      (flatmap (lambda (x)
                 (map (lambda (p) (cons x p))
                      (permutations (remove x s))))
               s)))
(define (remove item seq)
  (filter (lambda (x) (not (= x item)))
          seq))

EX 2.40

(define (unique-pairs n)
  (flatmap
   (lambda (i)
     (map (lambda (j) (list i j))
          (enumerate-interval 1 (- i 1))))
   (enumerate-interval 1 n)))
(define (new-prime-sum-pairs n)
  (map make-pair-sum
       (filter prime-sum? (unique-pairs n))))

EX 2.41

(define (sum-equal-s? triple s)
  (= s (+ (car triple) (cadr triple) (caddr triple))))
(define (make-triple n)
  (flatmap
   (lambda (i)
     (map (lambda (j) (cons i j))
          (unique-pairs (- i 1))))
   (enumerate-interval 1 n)))
(define (remove-not-equal triple s)
  (filter (lambda (pre-triple)
            (sum-equal-s? pre-triple s))
          triple))
(define (2-41 n s)
  (remove-not-equal (make-triple n) s))

EX 2.42

(define (queens board-size)
  (define (queen-cols k)  ;第k列
    (if (= k 0)
        (list empty-board)
        (filter
         (lambda (positions) (safe? k positions))
         (flatmap
          (lambda (rest-of-queens)
            (map (lambda (new-row)
                   (adjoin-position new-row k rest-of-queens))
                 (enumerate-interval 1 board-size)))
          (queen-cols (- k 1))))))
  (queen-cols board-size))

(define empty-board '())
(define (adjoin-position new-row k rest)
  (cons new-row rest))
(define (safe? k position)
    (iter-check (car position) 
                (cdr position)
                 1))

(define (iter-check row-of-new-queen rest-of-queens i)
    (if (null? rest-of-queens)  ; 下方所有皇后检查完毕,新皇后安全
        #t
        (let ((row-of-current-queen (car rest-of-queens)))
            (if (or (= row-of-new-queen row-of-current-queen)           ; 行碰撞
                    (= row-of-new-queen (+ i row-of-current-queen))     ; 右下方碰撞
                    (= row-of-new-queen (- row-of-current-queen i)))    ; 左下方碰撞
                #f
                (iter-check row-of-new-queen 
                            (cdr rest-of-queens)    ; 继续检查剩余的皇后
                            (+ i 1))))))            ; 更新步进值

;测试程序
(define testQueens
  (for-each (lambda (pos)
                    (begin
                        (display pos)
                        (newline)))
                (queens 8)))

SICP 2.2节习题(3)

发表于 2016-04-28 | 分类于 SICP解题集

第二章构造数据抽象

2.2 层次性数据和闭包性质

EX 2.33

accumulate中参数op是二元操作
lambda (x y) 中，x:(car seq) y:(accumulate op init (cdr seq))

;原始map定义
(define (map proc items)
  (if (null? items)
      '()
      (cons (proc (car items))
            (map proc (cdr items)))))

1
2
3

;用accumulate定义
(define (map1 p sequence)
  (accumulate (lambda (x y) (cons (p x) y)) '() sequence))

;原始append定义
(define (append list1 list2)
  (if (null? list1)
      list2
      (cons (car list1) (append (cdr list1) list2))))

1
2
3

;用accumulate定义
(define (append1 seq1 seq2)
  (accumulate cons seq2 seq1))

;原始length定义
(define (length items)
  (define (length-iter a count)
    (if (null? a)
        count
        (length-iter (cdr a) (+ 1 count)))))

1
2
3

;用accumulate定义
(define (length1 sequence)
  (accumulate (lambda (x y) (+ y 1)) 0 sequence))

EX 2.34

主要是采用Horner规则将多项式变形

“ex2-34”

(define (horner-eval x coefficient-sequence)
  (accumulate (lambda (this-coeff higher-terms) (+ this-coeff (* higher-terms x)))
              0
              coefficient-sequence))

EX 2.35

;原始count-leaves定义
(define (count-leaves t)
  (cond ((null? t) 0)
        ((not (pair? t)) 1)
        (else (+ (count-leaves (car t))
                 (count-leaves (cdr t))))))

;用accumulate定义
;map计算每一个结点的叶子数量,得到如(0 0 1 1 ......)的list，再累积便可
(define (count-leaves1 t)
  (accumulate + 0 (map
                   (lambda (x)
                     (if (pair? x)
                         (count-leaves1 x)
                         1))
                     t)))

EX 2.36

重点在于如何得到每一个内部序列的第一个元素，于是map一次seqs，对每个内部序列都得到其car

(define (accumulate-n op init seqs)
  (if (null? (car seqs))
      '()
      (cons (accumulate op init (map car seqs))
            (accumulate-n op init (map cdr seqs)))))

EX 2.37

;测试程序 矩阵1、2 向量1、2
(define test-matrix1 (list (list 1 2 3 4) (list 4 5 6 6) (list 6 7 8 9)))
(define test-matrix2 (list (list 1 4 6) (list 2 5 7) (list 3 6 8) (list 4 6 9)))
(define test-vector1 (list 1 2 3 4))
(define test-vector2 (list 4 5 6 6))

1
2
3

;求点积
(define (dot-product v w)
  (accumulate + 0 (map * v w)))

;矩阵乘向量，(矩阵列数 = 向量行数) 用map对每一行做点积
(define (matrix-*-vector m v)
  (map (lambda (row)
         (dot-product row v))
         m))

1
2
3

;求转置矩阵
(define (transpose mat)
  (accumulate-n cons '() mat))

;矩阵相乘
(define (matrix-*-matrix m n)
  (let ((cols (transpose n)))
    (map (lambda (row)
           (map (lambda (col)
                  (dot-product row col))
                cols))
         m)))

EX 2.38

书中fold-left过程如下

(define (fold-left op initial sequence)
  (define (iter result rest)
    (if (null? rest)
        result
        (iter (op result (car rest))
              (cdr rest))))
  (iter initial sequence))

从右向左对元素使用op操作，类似于accumulate

(define (fold-right op initial sequence)
  (if (null? sequence)
      initial
      (op (car sequence)
          (accumulate op initial (cdr sequence)))))

由几个例子可以看出，加法、乘法等满足结合律的op，对任何序列可以产生同样的结果

EX 2.39

;原始reverse
(define (reverse x)
  (define (iter remain result)
    (if (null? remain)
        result
        (iter (cdr remain) (cons (car remain) result))))
  (iter x '()))

(define (reverse1 sequence)
  (fold-right (lambda (x y) (append y (list x))) '() sequence))
(define (reverse2 sequence)
  (fold-left (lambda (x y) (cons y x)) '() sequence))

SICP 2.2节习题(2)

发表于 2016-04-21 | 分类于 SICP解题集

第二章构造数据抽象

2.2 层次性数据和闭包性质

EX 2.24

1	(define 2-24 (list 1 (list 2 (list 3 4))))

解释器打印出：

(1 (2 (3 4)))

盒子指针结构：

“ex2-24”

EX 2.25

(define a1 (list 1 3 (cons 5 7) 9))
(define 2-25-1
  (cdr (car (cdr (cdr a1)))))	;(cdr (car (cdr (cdr a1)))) 等价于 (cdaddr a1)

(define a2 (list (list 7)))
(define 2-25-2
  (car (car a2)))	;(car (car a2)) 等价于 (caar a2)

(define a3 (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7)))))))
(define 2-25-3
  (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr a3)))))))))))))	;等价于 (cadadr (cadadr (cadadr a3)))

EX 2.26

1 2	(define x (list 1 2 3)) (define y (list 4 5 6))

打印结果如下：

(append x y) -> (1 2 3 4 5 6)
(cons x y) -> ((1 2 3) 4 5 6)
(list x y) -> ((1 2 3) (4 5 6))

EX 2.27

;原始reverse
(define (reverse x)
  (define (iter rest result)
    (if (null? rest)
        result
        (iter (cdr rest) (cons (car rest) result))))
  (iter x '()))

;处理二叉树、三叉树等,如(list (list 2 1) (list 4 3) (list 6 5))
(define (deep-reverse x)
  (define (iter rest result)
    (if (null? rest)
        result
        (iter (cdr rest)
              (cons (if (pair? (car rest))
                        (deep-reverse (car rest))
                        (car rest))
                    result))))
  (iter x '()))

;一种更好的算法
(define (better-deep-reverse x)
  (if (pair? x)
      (reverse (map better-deep-reverse x))
      x))

EX 2.28

(define (fringe x)
  (cond ((null? x) '())
        ((not (pair? x)) (list x))
        (else (append (fringe (car x))	    ;left branch
                      (fringe (cdr x))))))	;right branch

EX 2.29

;原始构造函数
(define (make-mobile left right)
  (list left right))
(define (make-branch length structure)
  (list length structure))

;测试程序
(define lfbran (make-branch 1 2))
(define rtbran (make-branch 2 (make-mobile (make-branch 3 4) (make-branch 5 6))))
(define test-mobile (make-mobile lfbran rtbran))

a) 根据原始构造函数，不难写出选择函数

(define (left-branch mobile)
  (car mobile))
(define (right-branch mobile)
  (cadr mobile))
(define (branch-length branch)
  (car branch))
(define (branch-structure branch)
  (cadr branch))

b) total-weight 计算活动体总重量，递归地求和左右分支的总重量

(define (total-weight mobile)
  (+ (branch-weight (left-branch mobile))
     (branch-weight (right-branch mobile))))

(define (branch-weight branch)  ;计算分支重量
  (if (pair? (branch-structure branch))  ;是否吊着活动体
      (total-weight (branch-structure branch))
      (branch-structure branch)))

c) check-balance 检查二叉活动体是否平衡，递归判断左右分支是否平衡

(define (cal-torque branch)  ;计算分支力矩
  (* (branch-length branch) (branch-weight branch)))

(define (check-balance mobile)
  (if (null? mobile)
      #t
      (let ((left (left-branch mobile))
            (right (right-branch mobile)))
        (and (torque-equal? left right)
             (branch-balance? left)
             (branch-balance? right)))))

(define (torque-equal? lfbranch rtbranch)  ;力矩是否相等
  (= (cal-torque lfbranch) (cal-torque rtbranch)))

(define (branch-balance? branch)  ;分支是否平衡
  (if (pair? (branch-structure branch))  ;是否吊着活动体
      (check-balance (branch-structure branch))
      #t))

d) 这就是数据抽象的好处,改变构造方式,我们只需要修改相应的选择函数

(define (new-left-branch mobile)
  (car mobile))
(define (new-right-branch mobile)
  (cdr mobile))
(define (new-branch-length branch)
  (car branch))
(define (new-branch-structure branch)
  (cdr branch))

EX 2.30

;直接定义
(define (square-tree1 tree)
  (cond ((null? tree) '())
        ((not (pair? tree)) (square tree))
        (else (cons (square-tree1 (car tree))
                    (square-tree1 (cdr tree))))))

;map和递归定义
(define (square-tree2 tree)
  (map (lambda (sub-tree)
         (if (pair? sub-tree)
             (square-tree2 sub-tree)
             (square sub-tree)))
       tree))

EX 2.31

(define (tree-map proc items)
  (cond ((null? items) '())
        ((not (pair? items)) (proc items))
        (else (cons (tree-map proc (car items))
                    (tree-map proc (cdr items))))))
(define (square-tree3 tree)
  (tree-map square tree))

EX 2.32

求集合S的子集，就是求(cdr S)和(cdr S)里的每个元素append (car S)
例如S：(list 1 2 3)，子集是(() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))
先求(2 3)的子集，(() (3) (2) (2 3))，然后给每个append 1
具体递归分析如下：

“ex2-32”

(define (subsets s)
  (if (null? s)
      (list '())
      (let ((rest (subsets (cdr s))))
        (append rest (map (lambda (x) (cons (car s) x))
                           rest)))))

SICP 2.2节习题(1)

发表于 2016-04-21 | 分类于 SICP解题集

第二章构造数据抽象

2.2 层次性数据和闭包性质

EX 2.17

;返回列表尾元素
(define (last-pair x)
  (if (null? (cdr x))
      x
      (last-pair (cdr x))))

1 2	;测试 (last-pair (list 1 2 3 4))

EX 2.18

;反转列表
(define (reverse x)
  (define (iter remain result)
    (if (null? remain)
        result
        (iter (cdr remain) (cons (car remain) result))))
  (iter x '()))

EX 2.19

题目本身并不难，只要看过“换零钱”的程序，根据分治思想，分成使用的币种和为未使用的币种，两部分分别是list的car和cdr

;源程序
(define (cc amount coin-values)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (no-more? coin-values)) 0)
        (else (+ (cc amount (except-first-denomination coin-values))
                 (cc (- amount (first-denomination coin-values)) coin-values)))))

;补全程序
(define (first-denomination coin-values)
  (car coin-values))
(define (except-first-denomination coin-values)
  (cdr coin-values))
(define (no-more? coin-values)
  (null? coin-values))

EX 2.20

一般的思路是利用循环遍历列表，逐个判断元素的奇偶性，当该项符合要求时加入新的list中
这里的思路是抽象出一种通用的过程filter，体现了动态语言的特性，将过程(函数)作为参数传递

;P78 filter的定义
(define (filter predicate sequence)
  (cond ((null? sequence) '())
        ((predicate (car sequence))
         (cons (car sequence) (filter predicate (cdr sequence))))
        (else (filter predicate (cdr sequence)))))

;一种same-parity  
(define (same-parity x . y)
  (cond ((odd? x) (filter odd? (cons x y)))
        ((even? x) (filter even? (cons x y)))
        (else (display "x error"))))

;一种same-parity的简洁定义
(define (same-parity x . y)
  (filter (if (odd? x)
              odd?
              even?)
          (cons x y)))

EX 2.21

不难补全代码
第一种定义：对car项做平方，cdr项继续迭代回过程中
第二种定义：根据map的定义，形式参数是操作类型和被操作的项即可

;一种square-list的定义
(define (square-list1 items)
  (if (null? items)
      '()
      (cons (square (car items))
            (square-list1 (cdr items)))))

1
2
3

;另一种square-list的定义
(define (square-list2 items)
  (map square items))

EX 2.22

;原始程序(未交换cons参数)
(define (square-list items)
  (define (iter things answer)
    (if (null? things)
        answer
        (iter (cdr things)
              (cons (square (car things))
                    answer))))
  (iter items '()))

分析如下：

(square-list (list 1 2 3))                    ->
(iter (1 2 3) '())                            ->
(iter (2 3) (cons 1 '()))                    ->
(iter (3) (cons 4 (cons 1 '())))            ->
(iter '() (cons 9 (cons 4 (cons 1 '()))))    ->    (cons 9 (cons 4 (cons 1 '())))) = (list 9 4 1)
(9 4 1)

;原始程序(交换cons参数)
(define (square-list items)
  (define (iter things answer)
    (if (null? things)
        answer
        (iter (cdr things)
              (cons answer
                    (square (car things))))))
  (iter items '()))

分析如下：

(square-list (list 1 2 3))                    ->
(iter (1 2 3) '())                             ->
(iter (2 3) (cons '() 1))                    ->
(iter (3) (cons (cons '() 1) 4))            ->
(iter '() (cons (cons (cons '() 1) 4) 3))    ->    (cons (cons (cons '() 1) 4) 3) = (((() . 1) . 4) . 9)
(((() . 1) . 4) . 9)

;正确程序
(define (square-list items)
  (define (iter things answer)
    (if (null? things)
        (reverse answer)
        (iter (cdr things)
              (cons (square (car things))
                    answer))))
  (iter items '()))

分析如下：

(square-list (list 1 2 3))                    ->
(iter (1 2 3) '())                            ->
(iter (2 3) (cons 1 '()))                    ->
(iter (3) (cons 4 (cons 1 '())))            ->
(iter '() (cons 9 (cons 4 (cons 1 '()))))    ->    (cons 9 (cons 4 (cons 1 '()))) = (list 9 4 1)
(list 1 4 9)

EX 2.23

;类似于map的定义，返回逻辑值
(define (for-each proc items)
  (if (null? items)
      #f
      (cons (proc (car items))
            (for-each proc (cdr items)))))

SICP 2.1节习题(2)

发表于 2016-04-21 | 分类于 SICP解题集

第二章构造数据抽象

2.1 数据抽象引导

EX 2.7

(define (upper-bound x) (cdr x))

(define (lower-bound x) (car x))

(define (make-interval a b) (cons a b))

(define test (make-interval 1 2))

EX 2.8

1
2
3

(define (sub-interval x y)
  (make-interval (- (lower-bound x) (lower-bound y))
                 (- (upper-bound x) (upper-bound y))))

EX 2.9

显而易见，若两个区间分别为(1,2) (3,4)，被加宽度为0.5
对于加：(4,6)，宽度为0.5+0.5=1
对于减：(-2,-2),宽度为0.5-0.5=0
对于乘：p1=3 p2=4 p3=6 p4=8，(3,8), 宽度为2.5
对于除：第一个区间乘上第二个区间的倒数，p1=1/4 p2=1/3 p3=1/2 p4=2/3，(1/4,2/3)，宽度为5/24

EX 2.10

显然，如果两个区间分别为(0,1)，(1,2)
对于除：取倒数的时候可能会出现分母为0的情况
如果区间横跨0，区间取倒数的时候会出现上界小于下界的情况，(-1,2)取倒数后(1/2, -1)

(define (new-div-interval x y)
  (let ((y1 (lower-bound y))
        (y2 (upper-bound y)))
    (cond ((or (= y1 0) (= y2 0)) (display "error"))
          ((< y1 0) (display "error"))
          (else
           (mul-interval x
                         (make-interval (/ 1.0 y1)
                                        (/ 1.0 y2)))))))

SICP 2.1节习题(1)

发表于 2016-04-13 | 分类于 SICP解题集

第二章构造数据抽象

2.1 数据抽象引导

EX 2.1

(define (new-make-rat n d)
  (let ((g (gcd n d)))
    (cond ((or (and (< n 0) (< d 0)) (and (> n 0) (< d 0)))
           (cons (- (/ n g)) (- (/ d g))))
          (else (cons (/ n g) (/ d g))))))

“ex2-1”

EX 2.2

(define (make-segment start end)  ;构造函数make-segment
  (cons start end))

(define (start-segment segment)  ;选择函数start-segment
  (car segment))

(define (end-segment segment)  ;选择函数end-segment
  (cdr segment))

(define (make-point x y)	  ;构造函数make-point
  (cons x y))

(define (x-point point)  ;选择函数x-point
  (car point))

(define (y-point point)  ;选择函数y-point
  (cdr point))

;求线段中点
(define (midpoint-segment segment)
  (let ((start (start-segment segment))
        (end (end-segment segment)))
    (make-point (/ (+ (x-point start) (x-point end)) 2)
                (/ (+ (y-point start) (y-point end)) 2))))

;测试程序
(define start (make-point 1 3))
(define end (make-point 4 3))
(define seg (make-segment start end))
(define mid (midpoint-segment seg))

EX 2.3

两种矩形表示，一种采用两对线段(4条)，另一种采用两条相邻线段(2条)，主要设计抽象屏障，这里只采用后一种。当然还有别的表示方法，如三点表示(我没有仔细研究)

(define (make-rect seg1 seg2)  ;构造函数,构造矩形
  (cons seg1 seg2))
(define (seg1-in-rect rect)  ;选择函数,相邻的一条边a
  (car rect))
(define (seg2-in-rect rect)  ;选择函数,相邻的另一条边b
  (cdr rect))
(define (a-length rect)  ;a的长度
  (let ((a (seg1-in-rect rect)))
    (let ((a-startpt (start-segment a))
          (a-endpt (end-segment a)))
      (let ((a-x1 (x-point a-startpt))
            (a-y1 (y-point a-startpt))
            (a-x2 (x-point a-endpt))
            (a-y2 (y-point a-endpt)))
        (sqrt (+ (square (abs (- a-x1 a-x2))) (square (abs (- a-y1 a-y2)))))))))
(define (b-length rect)  ;b的长度
  (let ((b (seg2-in-rect rect)))
    (let ((b-startpt (start-segment b))
          (b-endpt (end-segment b)))
      (let ((b-x1 (x-point b-startpt))
            (b-y1 (y-point b-startpt))
            (b-x2 (x-point b-endpt))
            (b-y2 (y-point b-endpt)))
        (sqrt (+ (square (abs (- b-x1 b-x2))) (square (abs (- b-y1 b-y2)))))))))
(define (area-rect rect)	  ;计算面积,参数是矩形
  (let ((a (a-length rect))
        (b (b-length rect)))
    (* a b)))
(define (perimeter-rect rect)  ;计算周长,参数是矩形
  (let ((a (a-length rect))
        (b (b-length rect)))
    (* (+ a b) 2)))

;测试程序
;(define p1 (make-point 1 2))  ;p1 p2 p3,边不平行于坐标轴的矩形
;(define p2 (make-point 2 3))
;(define p3 (make-point 3 1))
(define p1 (make-point 1 1))	  ;p1 p2 p3,边平行于坐标轴的矩形
(define p2 (make-point 1 3))
(define p3 (make-point 5 1))
(define rectangle  ;测试所用的矩形
  (make-rect (make-segment p1 p2)
             (make-segment p1 p3)))

EX 2.4

根据代换法则，分析一下这种过程性表示方式

(define (cons x y)
  (lambda (m) (m x y)))
(define (car z)
  (z (lambda (p q) p)))

(car (cons x y))                        ——>
(car (lambda (m) (m x y)))                ——>
((lambda (m) (m x y)) (lambda (p q) p))    ——>
((lambda (p q) p) x y)                    ——>
x

代入具体的数字

(car (cons 1 2))            ——>
((lambda (p q) p) 1 2)        ——>
1

由代换结果分析，不难写出cdr的过程性表示

1 2	(define (cdr z) (z (lambda (p q) q)))

EX 2.5

(cons 2 3) = 108 = 2 * 2 * 3 * 3 * 3
将(cons 2 3)连续除以2，得到car。连续除以3，得到cdr

(define (cons x y)
  (* (expt 2 x) (expt 3 y)))

(define (car z)
  (if (= 0 (remainder z 2))
      (+ (car (/ z 2)) 1)
      0))

(define (cdr z)
  (if (= 0 (remainder z 3))
      (+ (cdr (/ z 3)) 1)
      0))

EX 2.6

根据书中给出的zero和add-1

(define zero 
  (lambda (f) (lambda (x) x)))
(define (add-1 n)
  (lambda (f) (lambda (x) (f ((n f) x)))))

推导出one(one = zero + add-1)

(add-1 zero)                                ——>
(add-1 (lambda (f) (lambda (x) x)))            ——>
(lambda (f) 
  (lambda (x) 
    (f (
      ((lambda (f) (lambda (x) x)) f) x))))    ——>
(lambda (f)
  (lambda (x)
    (f 
      ((lambda (x) x) x))))                    ——>
(lambda (f)
  (lambda (x)
    (f x)))                                    ——>
得到one的定义

(define one
  (lambda (f)
	(lambda (x)
	  (f x))))

同理，求two的定义。two = one + add-1

(add-1 one)                                    ——>
(add-1 (lambda (f) (lambda (x) (f x))))        ——>
(lambda (f)
  (lambda (x)
    (f ((n f) x))))                            ——>将n代换为one
(lambda (f)
  (lambda (x)
    (f ((
      (lambda (f) (lambda (x) (f x))) f) 
        x))))                                ——>化简lambda (f)
(lambda (f)
  (lambda (x)
    (f ( (lambda (x) (f x)) x))))            ——>化简lambda (x)
(lambda (f)
  (lambda (x)
    (f (f x))))                                ——>
得到two的定义

(define two
  (lambda (f)
    (lambda (x)
      (f (f x)))))

根据zero，one，two的定义

(define zero		;no f
  (lambda (f) 
	(lambda (x) 
	  x)))
(define one			;one f
  (lambda (f)
	(lambda (x)
	  (f x))))
(define two			;two f
  (lambda (f)
    (lambda (x)
      (f (f x)))))

据此推导加法过程定义(对此仍不太懂，没有理解FP，柯里化之类的内容)

(define church-add
  (lambda (m n)
	(lambda (f)
	  (lambda (x)
		(m f (n f x))))))

《计算机程序的解释和构造(SICP)》 (2)

发表于 2016-03-24 | 分类于 SICP

断断续续看完第一章的三节公开课，做完第一章的课后习题，回顾一下。

Lisp的基本语法
组合式的概念

例如: (+ 3 (* 5 6))
表达式类型
- numbers
- symbol
- lambda-expressions
- definitions
- conditionals(条件表达式)
- combinations(组合式)
  
  例如：
  1
  2
  (define a (* 5 5)) ;a是符号
  (define (a) (* 5 5)) ;a是过程
应用序和正则序

应用序：先求参后应用
正则序：先展开后规约
线性递归(Linear-Recurison)与迭代(Iteration)，时间复杂度、空间复杂度简单分析
函数式编程(functional programming)将过程(函数)作为参数，返回值等等

例如：

1
2
3

(define (compose f g)
  (lambda (x)
    (f (g x))))

复杂问题的分析与分解，划分成一个个自问题来解决
语法糖衣(syntactic sugar)
- lambda
  
  以下两种定义等价，都是f(x) = x + 1

1	(define (f x) (+ x 1))

1
2
3

(define f 
  (lambda (x) 
    (+ x 1)))

let

以下两种定义等价，都是f(x) = 2x + 1

(define (f x)
  ((lambda (a)		;a + x 
    (+ a x))
  (+ 1 x))		;a = x + 1

1
2
3

(define (f x)
  (let ((a (+ x 1)))	;a = x + 1
    (+ a x)))		;a + x

问题引入

常见的编码格式

Java中的编解码

IO中的编解码

内存中的编解码

Java中具体的编解码实例

几种编码格式的比较

PHP 5.6

Apache 2.4

WordPress

MySql 5.6

第二章 构造数据抽象

2.2 层次性数据和闭包性质

EX 2.40

EX 2.41

EX 2.42

第二章 构造数据抽象

2.2 层次性数据和闭包性质

EX 2.33

EX 2.34

EX 2.35

EX 2.36

EX 2.37

EX 2.38

EX 2.39

第二章 构造数据抽象

2.2 层次性数据和闭包性质

EX 2.24

EX 2.25

EX 2.26

EX 2.27

EX 2.28

EX 2.29

a) 根据原始构造函数，不难写出选择函数

b) total-weight 计算活动体总重量，递归地求和左右分支的总重量

c) check-balance 检查二叉活动体是否平衡，递归判断左右分支是否平衡

d) 这就是数据抽象的好处,改变构造方式,我们只需要修改相应的选择函数

EX 2.30

EX 2.31

EX 2.32

第二章 构造数据抽象

2.2 层次性数据和闭包性质

EX 2.17

EX 2.18

EX 2.19

EX 2.20

EX 2.21

EX 2.22

EX 2.23

第二章 构造数据抽象

2.1 数据抽象引导

EX 2.7

EX 2.8

EX 2.9

EX 2.10

第二章 构造数据抽象

2.1 数据抽象引导

EX 2.1

EX 2.2

EX 2.3

EX 2.4

EX 2.5

EX 2.6

第二章构造数据抽象

第二章构造数据抽象

第二章构造数据抽象

第二章构造数据抽象

第二章构造数据抽象

第二章构造数据抽象